Родителям

Решение логических задач

Мы много говорим о задачах, но почти ни слова не сказано о том, как решать логические задачи. Сегодня я хочу Вам рассказать, как решать задачи типа «Кто есть кто?». Такие задания очень разнообразны по сложности, содержанию и способам решения. Так какие же есть способы решения логических задач?

• Метод графов

Один из способов решения – решение с помощью графов. Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками. Пусть нам требуется установить соответствие между двумя типами объектов (множествами).

Пример. Леня, Женя и Миша имеют фамилию Орлов, Соколов и Ястребов. Какую фамилию имеет каждый мальчик, если Женя, Миша и Соколов – члены математического кружка, а Миша и Ястребов занимаются музыкой?

Решение. Решить задачу просто, если учесть, что каждому элементу одного множества обязательно соответствует элемент другого множества,но только один (у каждого мальчика есть фамилия и фамилии у мальчиков разные).

Прочитав внимательно условие, мы понимаем, что среди перечисленных  имен нет Лени, следовательно он - Соколов. Так же мы выясняем, что Ястребов - это Женя. Просто соединяйте элементы множеств между собой

Женя Миша Леня

Ястребов Соколов Орлов

• Табличный способ

Второй способ решения логических задач – с помощью таблиц – также прост и нагляден, но его можно использовать только в том случае, когда требуется установить соответствие между двумя множествами. Он более удобен, когда множества имеют по пять-шесть элементов.

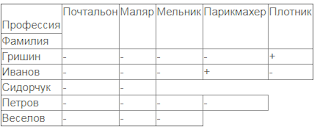
Пример. «Город мастеров». В нашем городе живут 5 друзей: Иванов, Петров, Сидорчук, Веселов и Гришин. У них разные профессии: маляр, мельник, парикмахер, почтальон, плотник. Но я точно знаю, что Петров и Гришин никогда не держали в руках малярной кисти, а Иванов и Гришин давно собираются посетить мельницу, где работает их товарищ. Петров и Веселов живут в одном доме с почтальоном. Иванов и Петров каждое воскресенье играют в городки с плотником и маляром, а Гришин и Веселов по субботам встречаются в парикмахерской, где работает их друг. Почтальон же предпочитает бриться дома. Помогите мне установить профессию каждого из друзей.

Решение. Решая задачу, мы заведомо знаем, что у каждого товарища одна фамилия и одна профессия (и у всех разные).

Правило 1. В каждой строке и в каждом столбце таблицы может стоять только один знак соответствия (например «+»).

Правило 2. Если в строке (или столбце) все «места», кроме одного, заняты одним символом, то на свободное место нужно поставить противоположный.

Начертив таблицу, нужно разместить в ней известные параметры исходя из условия задачи. Если ребята затрудняются сразу заполнить таблицу, то можно помочь им наводящими вопросами. 

После того, как произошло «сужение информации» и точно установлено, что Гришин – плотник, а Иванов – парикмахер, рассуждать можно так: т.к Иванов не почтальон (он парикмахер) и из условий задачи следует, что Гришин, Петров и Веселов не работают почтальоном, значит, Сидорчук – почтальон (а значит, не маляр и не мельник); мельником может быть только Петров, а Веселов – маляром. Эта задача предполагает только одно решение.

Как вы видите, решать задачи подобного рода не сложно. Главное представить условие схематически.